Authors: Steven Adriaensen*, Herilalaina Rakotoarison*, Samuel Müller, and Frank Hutter
TL;DR
In our paper, we propose LC-PFN, a novel method for Bayesian learning curve extrapolation. LC-PFN is a prior-data-fitted network (PFN), a transformer trained on synthetic learning curve data capable of doing Bayesian learning curve extrapolation in a single forward pass. We show that our approach is 10.000 faster than the state-of-the-art using MCMC (Domhan et al, 2015), without loss of performance, effectively enabling applications thereof in AutoML, at almost zero overhead.
Learning Curve Extrapolation
Arguably, what sets machine learning apart from other approaches to AI, is its ability “to improve its performance with experience” (Russel and Norvig, 2010). A learning curve (Mohr and van Rijn, 2022) characterizes the relationship between the performance of an agent as a function of its experience. For example, in deep learning, the learning curve typically describes the loss of the neural network model being trained as a function of the number of epochs it has been trained for. Here, learning curve extrapolation aims to predict model performance in later epochs of a machine learning training, based on the performance in the first epochs. These predictions are particularly useful in the context of AutoML, as they allow us to stop expensive training runs that will not produce models better than the best model seen thus far.


Being Bayesian about Learning Curves
Why? Learning curves are not always as smooth and predictable as those depicted above. Performance improvements may be non-monotonic (e.g., worsening steps), performance estimates noisy (e.g., mini-batch evaluations), learning may fail (e.g., divergence), or seem to fail and recover (e.g., double descent). In these cases, it may simply be impossible to confidently predict what exactly will happen.
What? Bayesian inference presents a general probabilistic framework for reasoning about uncertainty. Its essence is captured in Bayes’ Rule / Theorem:

In our case, hypotheses take the form of learning curves and evidence is presented as a partial learning curve until some cutoff T. While the equation gives us the posterior over learning curves, what we truly care about is the posterior predictive distribution (PPD), a distribution over model performances at epoch t’ > T, given we performances observed thus far, i.e., Bayesian prediction.
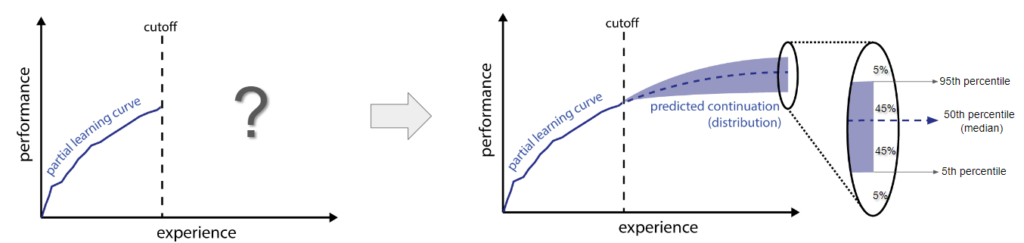
How? Before we can do Bayesian prediction, we need to define a prior. In our case, a prior over learning curves. As the name suggests, this distribution should ideally capture what we believe learning curves may look like, assigning high probability to those curves that are more likely to be observed than others. While coming up with a good learning curve prior is a challenging task in itself, it was not the main focus of our work, so we adopted the one from prior art (Domhan et al, 2015), with some modifications (see Section 3.2 the paper for all the technicalities). In a nutshell, Domhan et al (2015), modeled learning curves as linear combinations of monotonic basis curves, with additive Gaussian noise, and defined a prior over the parameters of this model, i.e., the weights and parameters for each basis curve, as well as the scale of the Gaussian noise. A sample of 10 curves from this prior is shown below.
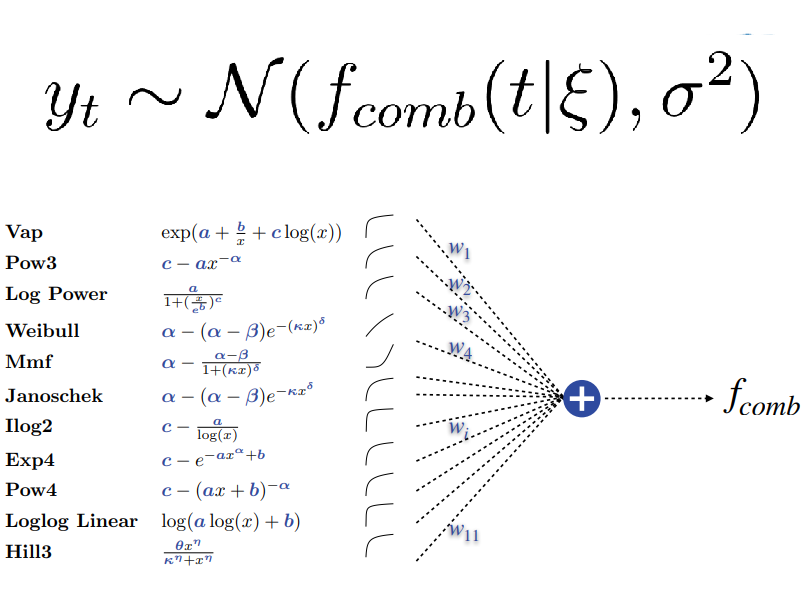
Now, in theory, given this prior and a partial learning curve, we can infer the posterior by applying Bayes’ rule. In practice, sadly, calculating the denominator in this equation (i.e., the marginal likelihood) exactly is often intractable and we must resort to approximate inference methods. Here, (Domhan et al, 2015) used Markov Chain Monte Carlo (MCMC). In our paper, we propose LC-PFN, an alternative approach using prior-data-fitted networks (PFNs, Mülller et al, 2021).
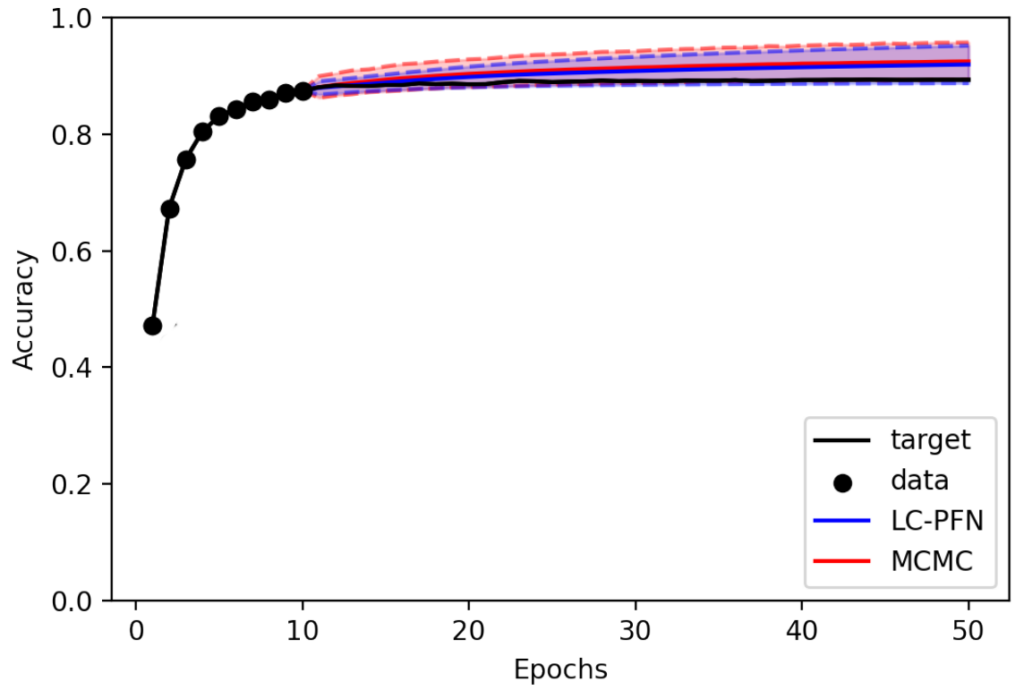
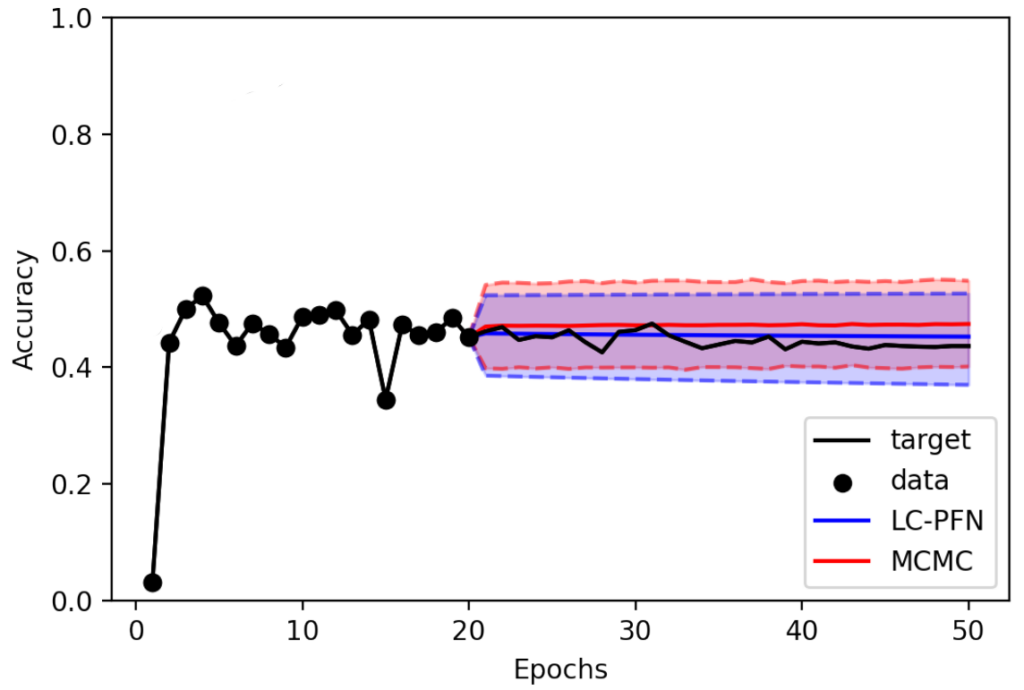
While the predictions of both methods are often similar, the true difference lies in the computational cost required to obtain them. The above inferences took about a minute using MCMC, but only a couple of milliseconds using LC-PFN (on CPU). While a minute may sound reasonable, it inhibits fine-grained, general-purpose applications in, e.g., AutoML systems.
PFNs, Transformers that can do Bayesian inference (efficiently)!
While various methods for ‘general’ approximate Bayesian inference exist (e.g., MCMC, Bayesian neural networks, (deep) Gaussian processes, variational inference, etc.), they are all either computationally expensive, or restrictive in terms of distributional assumptions, or both. Recently, Mülller et al (2021) proposed prior-data fitted networks (PFNs) an efficient and flexible approach to Bayesian inference.
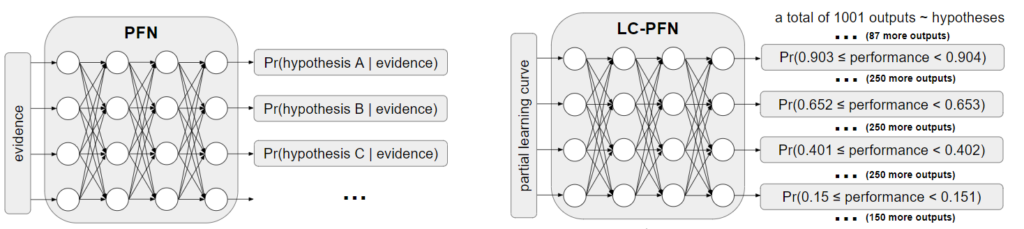
LC-PFN: Conceptually, PFNs are neural networks trained to do Bayesian inference in a single forward pass, i.e. given evidence (partial learning curve) as input, they can predict the likelihood of every given hypothesis.
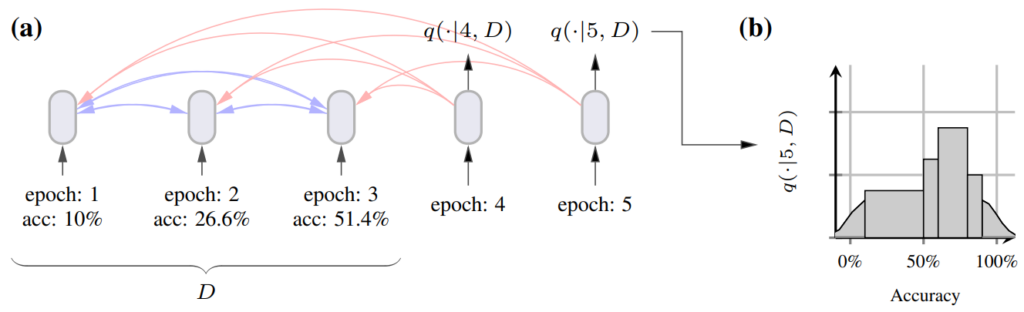
At training time, they are given masked examples sampled from the prior and must infer the masked-out part (minimizing log loss). In our case, LC-PFN is a decoder-only (GPT-style) transformer, trained on 10 million right-censored artificial learning curves that were sampled from the prior described above. Input tokens represent points (t, yt) of the partial learning curve (t < T). The output of the transformer for a query t’ > T-1 is a discretized version of the PPD for yt’.
Results: LC-PFN is Faster and Better!
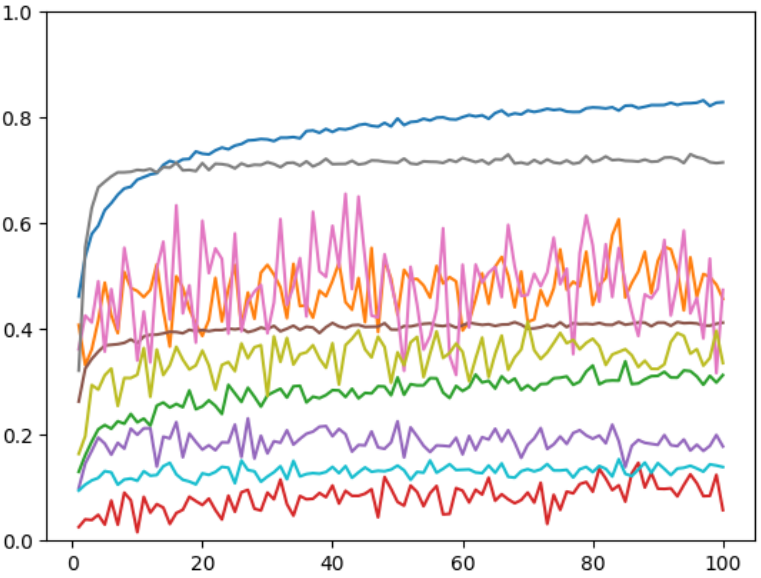
In the first experiment, we compare the existing MCMC and our LC-PFN approaches on artificial learning curves sampled from the prior. To analyze the effect of hyperparameters (and scale), we train different variants of each method. For a fair comparison, we ran method methods on CPU (despite LC-PFN running even faster on GPU).
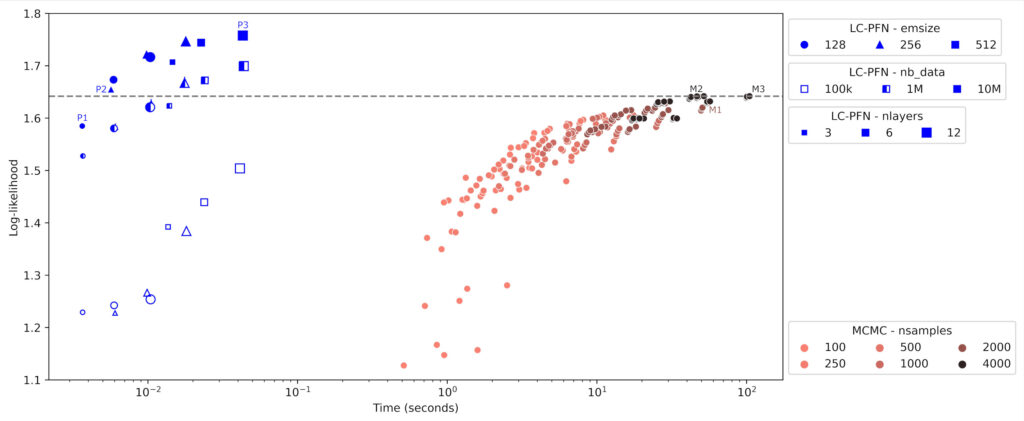

We find that all (but the smallest) LC-PFNs trained on 10M curves, outperform all MCMC variants in terms of PPD approximation, despite being multiple orders of magnitude faster. Unsurprisingly, we find that bigger is better for LC-PFN, at the cost of slightly slower inference. Note that training the
largest LC-PFN (P3, 10M samples with 26M parameters) on the prior took approximately eight hours
(single CPU, single RTX2080 GPU), but this cost is incurred only once for all of our experiments.
Results: LC-PFN works for real!
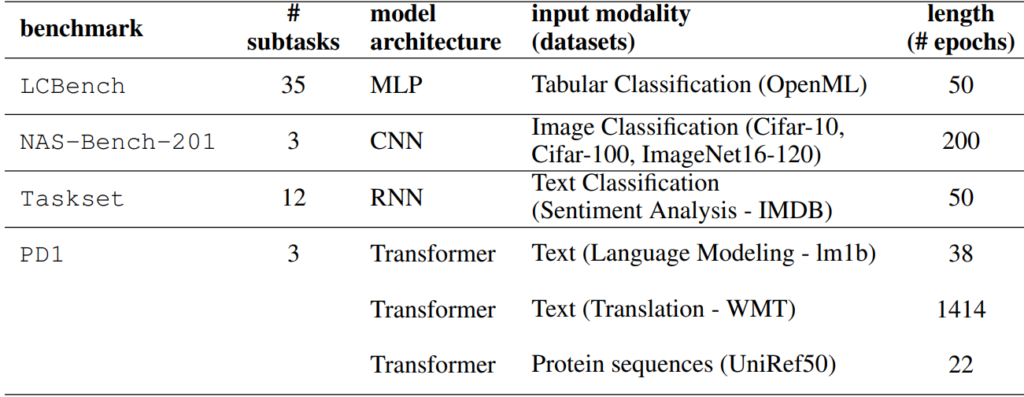
In a second experiment, we investigate the out-of-distribution (ood) performance of both methods, extrapolating 20.000 real learning curves sourced from four different benchmarks (LCBench, NAS-Bench-201, Taskset, and PD1) that stem from training a wide range of model architectures (MLPs, CNNs, RNNs, and Transformers) on 53 different datasets with varying input modalities (tabular, image, text, and protein data). To account for our modifications to the prior, we also include the variant using the original prior, in our comparison.
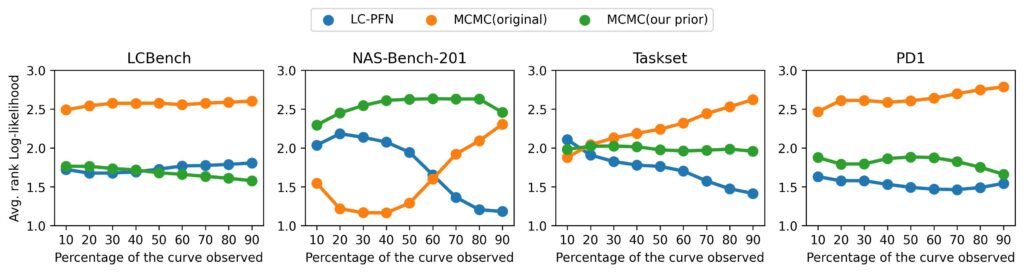
We find that while LC-PFN does not always produce the best extrapolation, it arguably still is (across all benchmarks) preferable among the three approaches compared, despite being multiple orders of magnitude faster.
Results: LC-PFN, can it be stopped?!
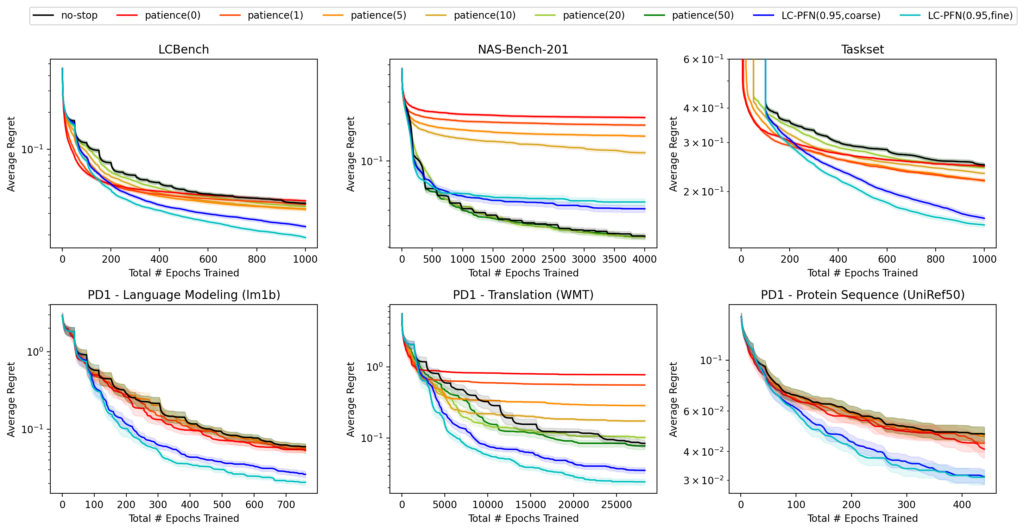
Finally, to get an idea of how practically useful the LC-PFN’s extrapolations are in the context of AutoML, we evaluate its use in a predictive early-discarding criterion in the context of vertical model selection. Here, multiple training runs (~ learning curves) for a task (using different hyperparameters) are considered in a predetermined order, and we must decide whether to continue the current training or stop and start the next training. As we consider a limited budget of 20 full training runs, stopping non-promising runs early is essential. We stop a run, once LC-PFN predicts the likelihood of obtaining a model better than the best one found thus far is less than 5%.

In our experiments, we observed a 2-6 factor speedup (compared to not stopping) on 45 of the 53 tasks considered. We only observed slowdowns on the 3 NAS-Bench-201 tasks, however, most learning curves in this benchmark are very unlikely under our prior, hence this failure can likely be attributed to the choice of learning curve prior, not LC-PFN.
Try LC-PFN yourself!
All our trained LC-PFN models, as well as code to train them, can be found on Github.
Don’t like code? Check out our code-free demo on Hugging Face!
References
(Domhan et al, 2015) Domhan, T., Springenberg, J. T., & Hutter, F. (2015, June). Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. In Twenty-fourth international joint conference on artificial intelligence.
(Russel and Norvig, 2010) Russell, S. J., & Norvig, P. (2010). Artificial intelligence a modern approach. London.
(Mohr and van Rijn, 2022) Mohr, F., & van Rijn, J. N. (2022). Learning Curves for Decision Making in Supervised Machine Learning–A Survey. arXiv preprint arXiv:2201.12150.
(Müller et al, 2021) Müller, S., Hollmann, N., Arango, S. P., Grabocka, J., & Hutter, F. (2021, October). Transformers Can Do Bayesian Inference. In International Conference on Learning Representations.