Image Credit: Ina Lindauer
Hyperparameter optimization is a powerful approach to achieve the best performance on many different problems. However, classical approaches to solve this problem all ignore the iterative nature of many algorithms. Dynamic algorithm configuration (DAC) is capable of generalizing over prior optimization approaches, as well as handling optimization of hyperparameters that need to be adjusted over multiple time-steps. To allow us to use this framework, we need to move from the classical view of algorithms as a black-box to more of a gray or even white-box view to unleash the full potential of AI algorithms with DAC.
Our benchmark library for DAC provides such gray- and white-box versions of several target algorithms from several domains, including AI Planning, Evolutionary Computation and Deep Learning.
Blog Post
Dynamic Algorithm Configuration for AI Planning
AI Planning makes use of heuristics to search for well performing solutions. For the various different problem domains that can be tackled with AI planning, a user can choose from a variety of heuristics. Some of these heuristics are more suited to certain problem instances and domains than others. Thus, it has become common in AI planning to employ portfolio approaches to try and select the best suited heuristic for the problem at hand. However, such approaches do not take into account that during the search different heuristics might be better suited.
Dynamic algorithm configuration can be used to learn to switch between heuristics depending on some internal statistics of the planning system. For example, tracking simple statistics that show how the heuristics themselves perform allows DAC to learn dynamic policies that are capable of switching between heuristics during the search. We could theoretically and empirically show that such flexible dynamic policies are capable of outperforming the theoretical best possible algorithm selector.
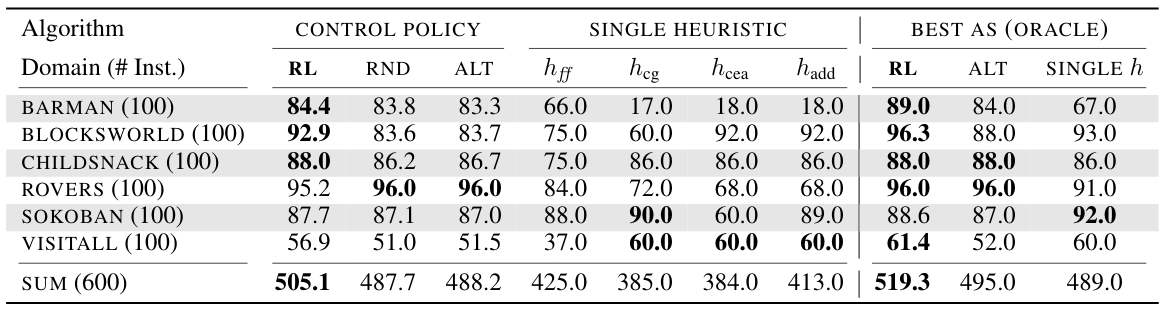
Number of solved problem instances. RL corresponds to a learned DAC policy. RND and ALT are two handcrafted dynamic policies. On the problem domains Barman and Childsnack the DAC policies (first column) outperform the theoretically best possible algorithm selector (last column).
Dynamic Algorithm Configuration for Evolutionary Algorithms
In CMA-ES, the step size controls how fast or slow a population traverses through a search space. Large steps allow you to quickly skip over uninteresting areas (exploration), whereas small steps allow a more focused traversal of interesting areas (exploitation). Handcrafted heuristics usually trade off small and large steps given some measure of progress. Directly learning in which situation which step-size is preferable would allow us to act more flexible than a hand-crafted heuristic could. To learn such dynamic configuration policies, one approach is dynamic algorithm configuration through the use of reinforcement learning.
Through the use of DAC we could learn policies that are capable of generalizing beyond the training setting. DAC policies could transfer the learned step-size adaptation to functions of higher dimensions, over longer optimization trajectories of CMA-ES as well as other function classes.
Dynamic Algorithm Configuration on Artificial Functions
In our earliest work on dynamic algorithm configuration (DAC) we introduced the framework itself and presented the formulation of dynamic configuration as a contextual Markov Decision Process (cMDP). Based on this formulation, we proposed and evaluated solution approaches based on reinforcement learning.
To properly study the effectiveness and limitations of these approaches, we introduced artificial benchmarks that have very low computational overhead while enabling evaluation of DAC policies with full control over all aspects and characteristics of the environment. Specifically, we designed the Sigmoid and Luby benchmarks.
Sigmoid, as the name implies, is based on the sigmoid function $latex sig(t) = \frac{1}{1 + e^{-t}}$.
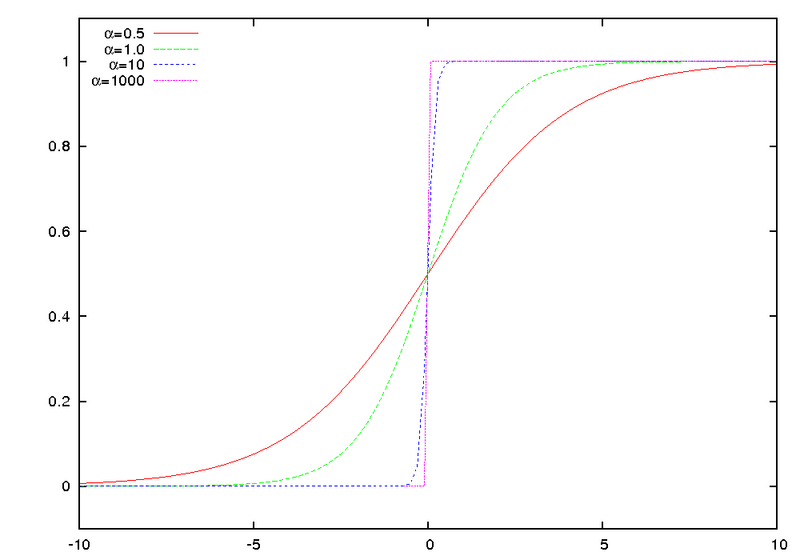
Effect of the scaling factor (here $latex \alpha$) on sigmoid functions all with inflection point $latex 0$. (Original from Wikimedia)
However, to allow for the notion of problem instances in this benchmark, we introduced the notion of context features.
These features (aka meta-features in other settings) enable us to easily distinguish one problem instance from another.
For example, the feature “height” would let help you distinguish mountains from each other.
For Sigmoid the context features are the scaling factor $latex s_{i, h}$ and the inflection point $latex p_{i, h}$, which depend on the problem instance at hand $latex i$ and the hyperparameter dimension $latex h$. With these features, we can construct complex Sigmoid functions that are shifted along the time axis $latex t$ and exhibit different scaling factors. Further, by basing the context features on the hyperparameter dimension, we can study the ability of dynamic configuration policies in configuring multiple parameters at once.
The resulting Sigmoid thus is $latex sig(t; s_{i, h},p_{i, h})= \frac{1}{1 + e^{-s_{i, h}\cdot(t – p_{i, h})}}$.
The second benchmark Luby is based on the luby sequence which is 1,1,2,1,1,2,4,1,1,2,1,1,2,4,8,…; formally, thet-th value inthe sequence can be computed as:
$latex l_t = \left\{\begin{array}{ll}2^{k-1}& \mathrm{if }\,t = 2^k – 1,\\l_{t – 2^{k – 1} + 1}& \mathrm{if }\,2^{k-1}\leq t < 2^k – 1.\end{array}\right.$
Again we can introduce context features to modify the original sequence. For example, we introduced a “short effective sequence length” $latex L$. This value tells us how many correct actions need to be played before an instance is deemed solved. Every incorrect choice will than require at least one additional action to counteract the wrong choices.
If you want to play around with the proposed benchmarks and some simple RL agents that can learn to solve them,
checkout the source code. You can also checkout the video presentation at ECAI’20:
Full List of Publications on DAC by Our Groups
- S. Adriaensen and A. Biedenkapp and G. Shala and N. Awad and T. Eimer and M. Lindauer and F. Hutter
Automated Dynamic Algorithm Configuration
In: Journal of Artificial Intelligence Research (JAIR) 2023
Link to source code
- A. Biedenkapp and D. Speck and S. Sievers and F. Hutter and M. Lindauer and J. Seipp
Learning Domain-Independent Policies for Open List Selection
In: Workshop on Bridging the Gap Between AI Planning and Reinforcement Learning (PRL @ ICAPS’22)
- A. Biedenkapp and N. Dang and M. S. Krejca and F. Hutter and C. Doerr
Theory-inspired Parameter Control Benchmarks for Dynamic Algorithm Configuration
In: Proceedings of the Genetic and Evolutionary Computation Conference (GECCO’22)
Won the best paper award (GECH track)
Link to source code
- T. Eimer and A. Biedenkapp and M. Reimer and S. Adriaensen and F. Hutter and M. Lindauer
DACBench: A Benchmark Library for Dynamic Algorithm Configuration
In: Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI’21)
Link to source code of DACBench and accompanying blog post.
Link to the video presentation at IJCAI’21.
- D. Speck and A. Biedenkapp and F. Hutter and R. Mattmüller and M. Lindauer
Learning Heuristic Selection with Dynamic Algorithm Configuration
In: Proceedings of the Thirty-First International Conference on Automated Planning and Scheduling (ICAPS’21)
Link to source code and data of using DAC to switch heuristics in AI planning.
Link to the video presentation for a workshop version of the paper presented at PRL@ICAPS’20.
- G. Shala and A. Biedenkapp and N. Awad and S. Adriaensen and M. Lindauer and F. Hutter
Learning Step-Size Adaptation in CMA-ES
In: Proceedings of the Sixteenth International Conference on Parallel Problem Solving from Nature (PPSN’20)
Link to source code and data as well as trained policies and accompanying blog post.
Link to the video poster presentation at PPSN’20. - A. Biedenkapp and H. F. Bozkurt and T. Eimer and F. Hutter and M. Lindauer
Dynamic Algorithm Configuration: Foundation of a New Meta-Algorithmic Framework
In: Proceedings of the Twenty-fourth European Conference on Artificial Intelligence (ECAI’20)
Link to source code of usage of DAC on artificial benchmarks. Link to accompanying blog post.
Link to the video presentation at ECAI’20. - A. Biedenkapp and H. F. Bozkurt and F. Hutter and M. Lindauer
Towards White-box Benchmarks for Algorithm Control
In: DSO Workshop@IJCAI’19
Note: In this early work we referred to DAC as “Algorithm Control”
Related Topics
https://www.automl.org/automated-algorithm-design/algorithm-selection/