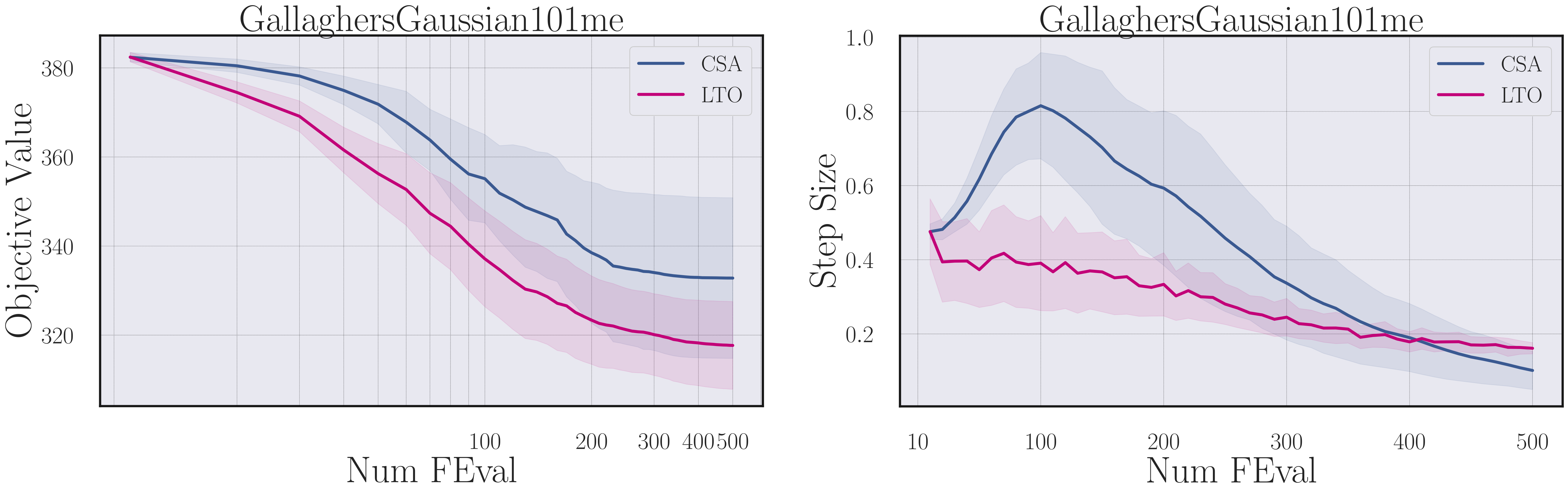
In a Nutshell
In CMA-ES, the step size controls how fast or slow a population traverses through a search space. Large steps allow you to quickly skip over uninteresting areas (exploration), whereas small steps allow a more focused traversal of interesting areas (exploitation). Handcrafted heuristics usually trade off small and large steps given some measure of progress. Directly learning in which situation which step-size is preferable would allow us to act more flexible than a hand-crafted heuristic could. To learn such dynamic configuration policies, one approach is dynamic algorithm configuration (DAC) through the use of reinforcement learning.
Learning vs. Hand-Crafting Policies
When designing heuristics, a developer usually has a specific task or family of tasks in mind which she would like to solve (better) through the use of that heuristic. Additionally, designing heuristics that guide an algorithm over long horizons is also very difficult. As a developer you might expect a certain stochasticity or other landscapes of your search space without taking into account that this search space might be much more dynamic and temporally look vastly different.
By automating the design or choice of a heuristic (i.e. learning it) it is much easier to expose the reinforcement learning system to a larger variety of example search spaces. However, completely starting to learn a heuristic from scratch can be a very difficult task for any learning system, especially if we want to be able to tackle many different problem spaces.
Getting the Best of Both Approaches
Combining both approaches, i.e. hand-crafted expert knowledge and a learning system should allow us to combine the strengths of both.
However, prior DAC methods [1,2,3] made use of value-based reinforcement learning (RL) methods. Such methods need to learn a value-function to be able to find a well performing policy. To be able to start from a reasonable value-function, we would need extensive prior knowledge of the reward signal that we are optimizing. Thus, value-based RL methods can not easily incorporate prior knowledge. As hand-crafted heuristics for step-size adaptation themselves are policies, we instead can turn to policy search methods.
The approach we explore in our paper “Learning Step-Size Adaptation in CMA-ES”, is to use the hand-crafted expert knowledge as a starting point for our policy-search based reinforcement learning agent. One way of incorporating such expert knowledge is through imitation learning, which it is known to be a very useful tool, especially in the robotics community. However imitation learning by itself is concerned with learning policies that behave exactly like the hand-crafted ones and can only ever become as good as the teacher examples.
How Can We Combine Both Approaches?
This shortcoming of pure imitation learning can easily be circumvented using Guided Policy Search (GPS) [4] which allows to start by imitating a teacher before following the reward signal.
As we have stated in our paper:
In essence GPS learns arbitrary parameterized policies through supervised learning
by fitting a policy to guiding trajectories [4, 5] From [hand-crafted example policies], a
teacher distribution is computed such that it maximizes the reward and the
agreement with the current policy. The policy parameters are then updated in a
supervised fashion such that new sample trajectories produced by the policy do
not deviate too far from the teacher. For a detailed explanation we refer to [5].
Thus GPS provides us with a rather elegant way of starting from expert knowledge while allowing us to follow some reward signal to further improve our learned policies.
But the “standard” GPS setting assumes that we have a fixed set of initial teaching examples and not “unlimited access” to the teachers responsible for generating these examples.
In its standard setting, GPS has been used in “Learning to Optimize” [6] to learn a better optimization algorithm. Unlike DAC, in this line of work, the learned algorithm is trained to directly output the next step in the problem space. With DAC however, we are interested in learning heuristics/policies that act in the parameter space, thereby influencing the behavior of another algorithm which then in turn acts in the problem space.
Fortunately, in our setting, where we care about step-size adaptation mechanisms in CMA-ES, we are able to continuously query the default adaptation mechanism (CSA) and observe how it would behave in different situations. As we would like to learn a dynamic controller that can handle a large variety of different situations, this means we can query the hand-crafted expert policy to show us how it would potentially act in new and unseen situations. During training, this allows our learned policy to learn about the strengths of the hand-crafted expert and imitate it where it is acting optimally but also to learn better behavior based on some reward signal.
How Much Should We Depend on Expert Knowledge?
In order to use GPS in our setting where we can continuously query an expert for examples, we need to balance imitating the expert and following the reward signal. If we purely focus on the expert examples, we end up with standard imitation learning, and if we only sample once in the beginning, we recover the standard GPS setting. Through a simple sampling rate we modify GPS to balance both aspects. In our experiments it turns out that it is best to mostly follow the reward signal, but also to regularly query the expert such that ~30% of the examples are generated by the hand-crafted expert.
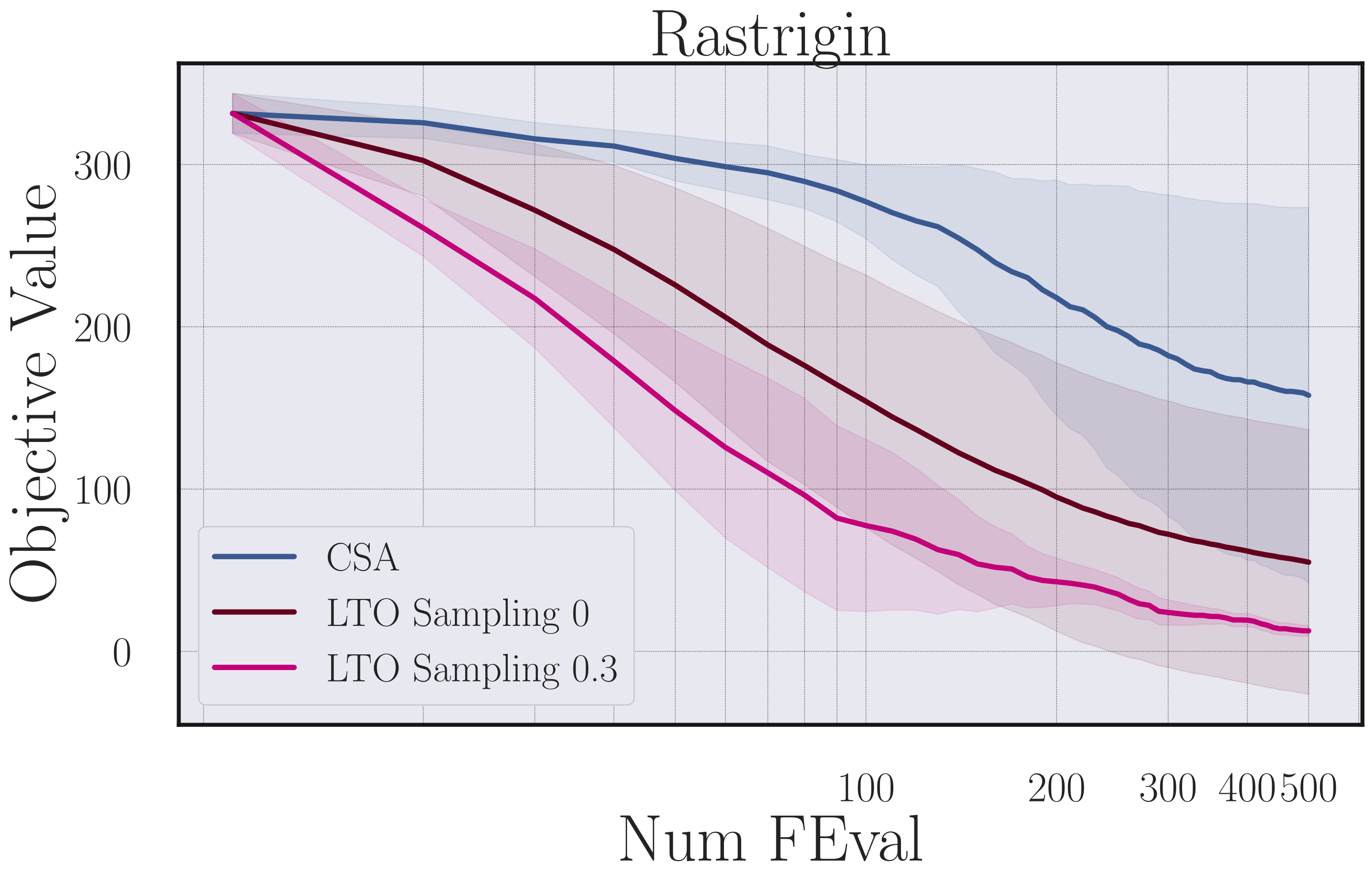
Difference in CMA-ES objective value for policies learned with different sampling rates (0 -> pure GPS and 1 -> hand-crafted heuristic “CSA”).
Does it Generalize?
We repeatedly stated that a learned system/policy has the advantage that it can more flexibly adapt to a broader variety of tasks. To show that this statement is actually true, we evaluate different scenarios of generalization:
- Generalization to different dimensional target functions
- Generalization to longer optimization horizons
- Generalization to completely unseen test functions
Without going into too much detail, the short answer is that the learned policies are able to generalize in all of these dimensions, at least to some degree. For the long and detailed answer we refer you to the paper itself.
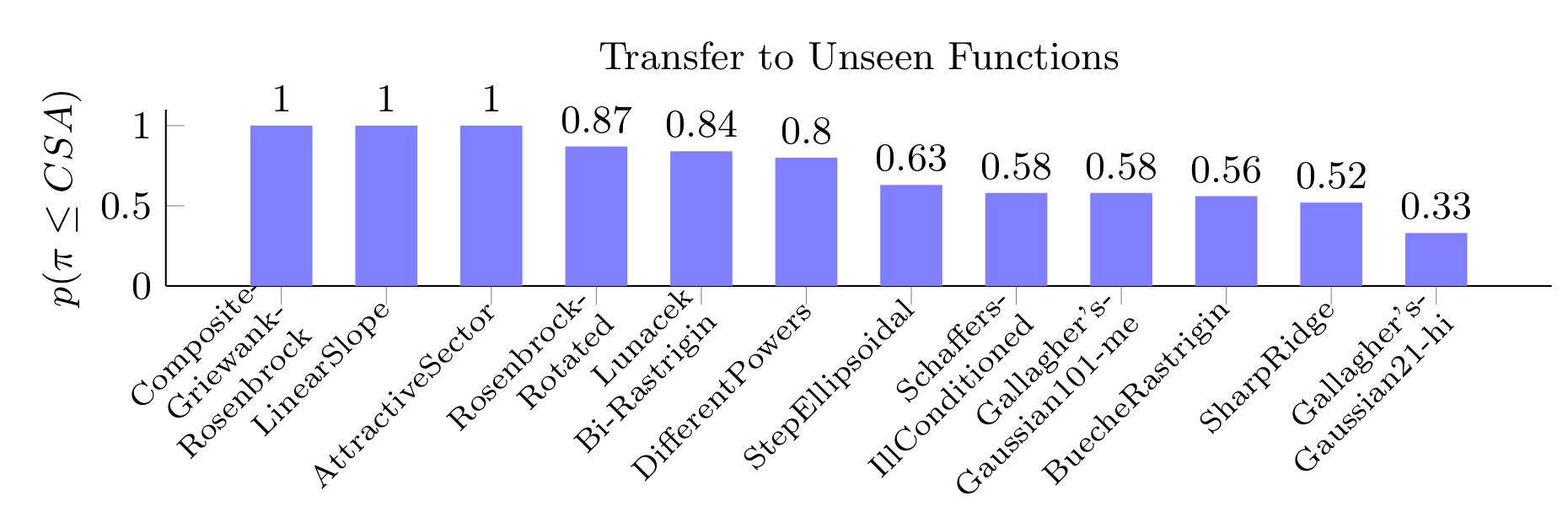
Fraction of runs that our learned heuristic outperformed the baseline heuristic (CSA) on unseen test functions.
Take Home Message
For a variety of algorithms, many expert researchers and developers have created an abundance of heuristics to dynamically modify an algorithm’s behavior. These heuristics most often come with some bias that tailors them to solve specific problems optimally. Moving from manual to automatic design of such heuristics, the knowledge enclosed within such heuristics makes for the ideal starting point to learn more flexible behavior. Prior approaches to DAC based on value-based RL cannot easily incorporate such prior knowledge. Instead, using guided policy search we are able to learn policies by starting from hand-crafted heuristics. Furthermore, in this optimization setting we are able to continuously query the hand-crafted heuristic to see how it behaves in new and unseen situations. This allows us to learn policies that are better at exploiting strengths of hand-crafted experts.
If you are interested to learn more about the method, check out the paper as well as the code.
If you are keen to learn more about DAC, read our earlier blog post and check our DAC website which we keep up to date with our newest work on DAC.
References
[1] A. Biedenkapp and H. F. Bozkurt and T. Eimer and F. Hutter and M. Lindauer
Dynamic Algorithm Configuration: Foundation of a New Meta-Algorithmic Framework
In: Proceedings of ECAI20
[2] D. Speck and A. Biedenkapp and F. Hutter and R. Mattmüller and M. Lindauer
Learning Heuristic Selection with Dynamic Algorithm Configuration
In: arXiv:2006.08246 [cs.AI]
[3] Sharma, M., Komninos, A., López-Ibáñez, M., Kazakov, D.:
Deep reinforcement learning based parameter control in differential evolution.
In: Proceedings of the Genetic and Evolutionary Computation Conference. pp. 709–717 (2019)
[4] Levine, S., Koltun, V.:
Guided policy search.
In: Dasgupta, S., McAllester, (eds.) Proceedings of the 30th International Conference on Machine Learning (ICML’13). pp. 1–9. Omnipress (2013)
[5] Levine, S., Abbeel, P.:
Learning neural network policies with guided policy search under unknown dynamics.
In: Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K. (eds.) Proceedings of the 28th International Conference on Advances in Neural Information Processing Systems (NeurIPS’14). pp. 1071–1079 (2014)
[6] Li, K., Malik, J.:
Learning to optimize.
In: Proceedings of the International Conference on Learning Representations (ICLR’17) (2017),
published on-line: iclr.cc