LC-PFN

Efficient Bayesian Learning Curve Extrapolation using PFNs

AutoML has revolutionized the field of machine learning by automating the process of model selection, hyperparameter tuning, and feature engineering. It has made it more accessible for non-experts to leverage the power of machine learning in their applications. However, one of the challenges in AutoML is the computational cost associated with evaluating a large number of models and their hyperparameter configurations. Furthermore, with the modern “Bigger is Better” trend in deep learning and large language models (LLMs), training is becoming increasingly more expensive, rendering AutoML intractable.

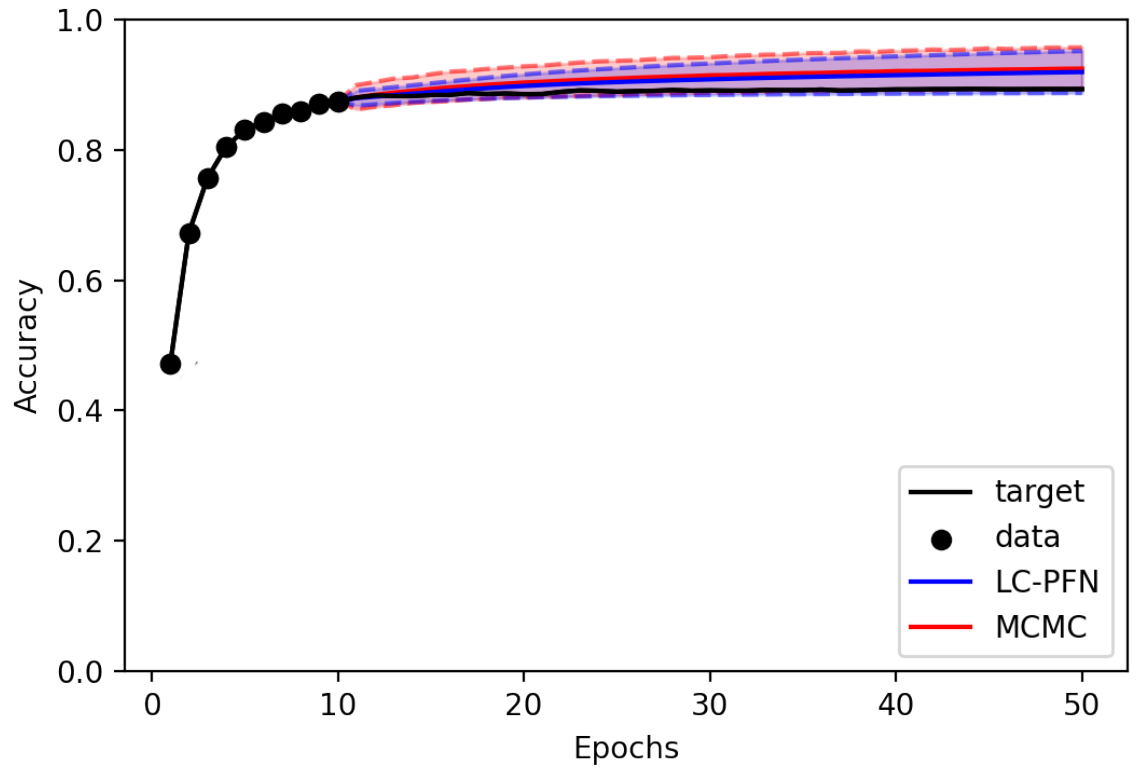
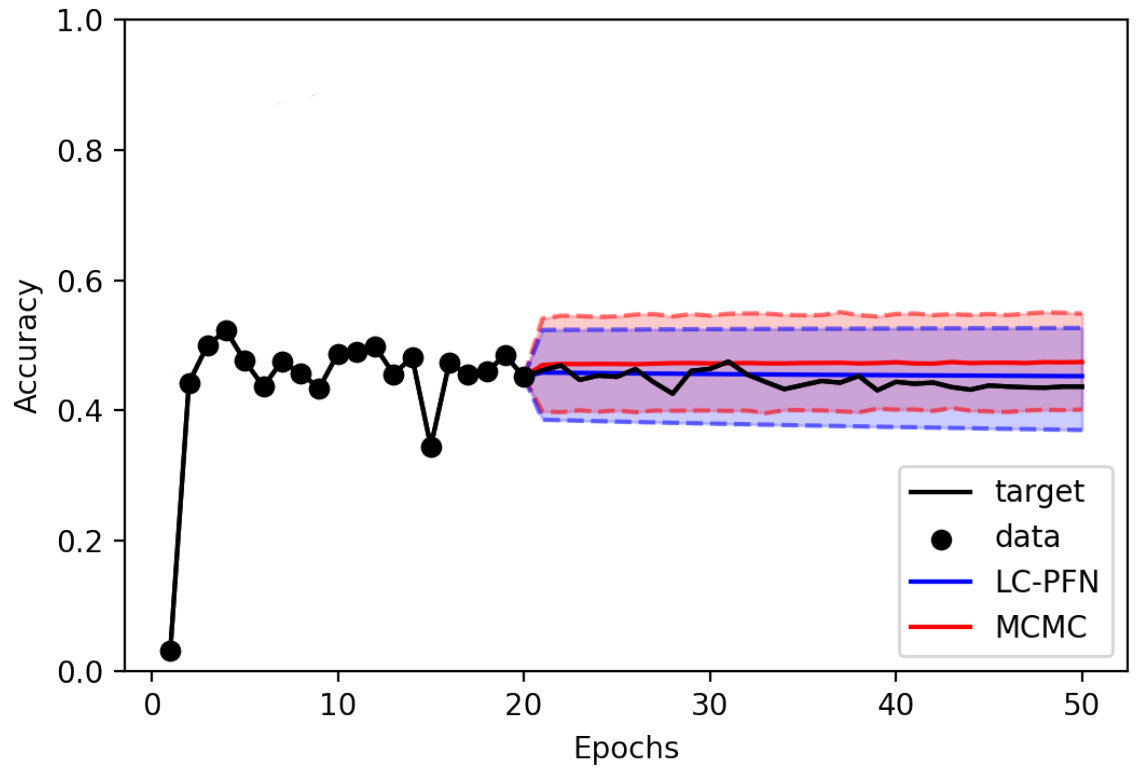
Learning curve extrapolation aims to predict model performance in later epochs of a machine learning training, based on the performance in the first epochs. These predictions are particularly useful in the context of AutoML, as they allow us to stop expensive training runs that will not produce models better than the best model seen thus far. However, while many learning curves are well-behaved (i.e., predictable), some exhibit chaotic behavior and are intrinsically difficult to accurately predict, warranting a Bayesian approach that also estimates the reliability of its predictions. However, existing Bayesian approaches to learning curve extrapolation are themselves costly (e.g., using MCMC, Bayesian Neural Networks) and/or inflexible (e.g., using Gaussian Processes), adding significant overhead.

LC-PFN is a novel, efficient and flexible approach to Bayesian Learning curve extrapolation. LC-PFN is a transformer, pre-trained on artificial learning curve data generated from a prior, to perform approximate Bayesian learning curve extrapolation in a single forward pass. Preliminary results show that LC-PFNs can approximate the posterior predictive distribution over learning curves more accurately and multiple orders of magnitude faster than MCMC, using the same prior, as well as obtaining competitive performance out-of-distribution, on real learning curve data from LCBench.

References

• Steven Adriaensen, Herilalaina Rakotoarison, Samuel Müller, and Frank Hutter
  Efficient Bayesian Learning Curve Extrapolation using Prior-Data Fitted Networks
  In: Proceedings of the 37th Conference on Neural Information Processing Systems (NeurIPS 2023)., New Orleans (link to full paper PDF).
• Steven Adriaensen, Herilalaina Rakotoarison, Samuel Müller, and Frank Hutter
  Efficient Bayesian Learning Curve Extrapolation using Prior-Data Fitted Networks
  In: 6th Workshop on Meta-Learning at NeurIPS 2022, New Orleans (link to workshop paper PDF).