By
Most work on neural architecture search (NAS, see our recent survey) solely optimizes for one criterion: high performance (measured in terms of accuracy). This often results in large and complex network architectures that cannot be used in real-world applications with several other important criteria including memory requirement, energy consumption and latency. The other problem in many traditional NAS methods (such as evolutionary, RL or Bayesian Optimization) is that they require enormous computational costs: running these methods entails training hundreds to thousands of neural networks from scratch, making the development phase very expensive and limiting research on them to a few research groups with massive compute resources.
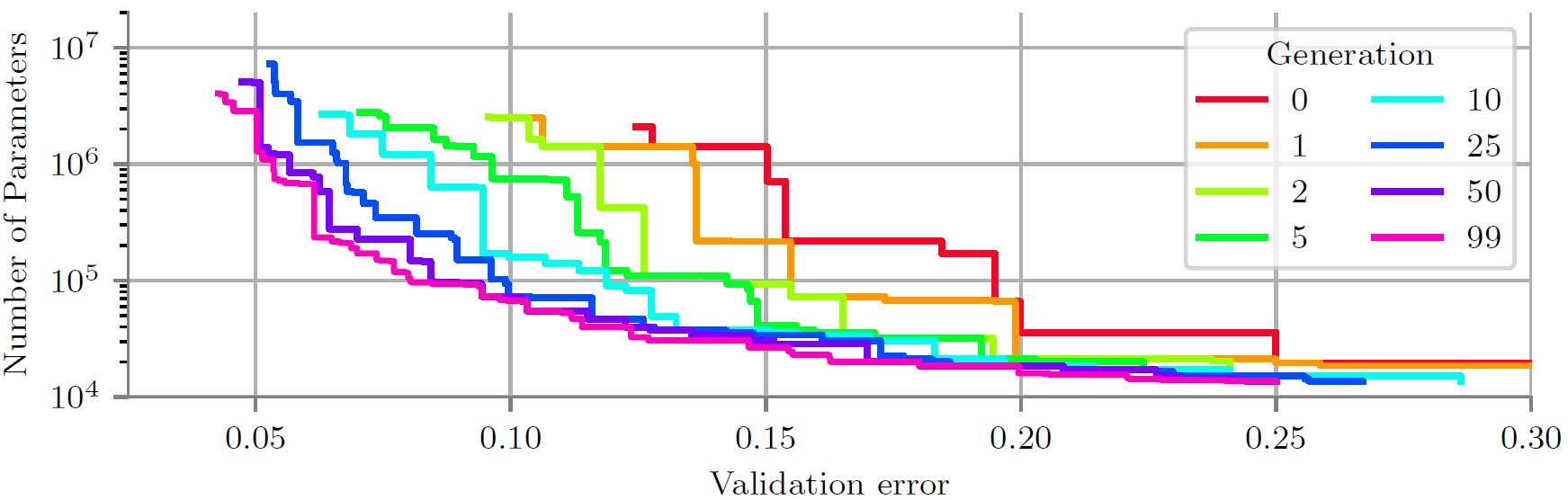
Figure 1: In this example, LEMONADE concurrently minimizes two objectives: validation error and number of parameters. Starting from trivial but poorly-performing networks in generation 0, the population improves over the course of LEMONADE with respect to both objectives. Each colored line denotes the performance of the population from each iteration / generation.
In our ICLR 2019 paper Efficient Multi-Objective Neural Architecture Search via Lamarckian Evolution, we proposed an algorithm called LEMONADE (Lamarckian Evolutionary for Multi-Objective Neural Architecture DEsign) to deal with both of these problems. On a high level, LEMONADE is a simple evolutionary algorithm for optimizing multiple objectives such as accuracy, memory requirements and latency.
LEMONADE starts from an initial population, i.e., an initial set of very simple neural networks. In every iteration, it then executes the following steps:
- Sample networks from the population (these will become the parents of the networks of the next generation).
- Generate children by applying mutations to the parent networks. In the context of neural networks, mutations denote operations such as adding or removing a layer, adding or removing a skip connection and increasing or decreasing the number of filters in a convolutional layer.
- Evaluate these children with respect to the multiple objectives.
- Update the population. In our case, we define the population to consist of all non-dominated networks from the previous population and the generated children. A neural network X is non-dominated, if and only if there is no other network Y that outperforms X with respect to all objectives.
LEMONADE is an anytime algorithm and iterates these four steps until it is out of time.
How does LEMONADE deal with the two problems we mentioned in the beginning? The multi-objective part is simple: step 4 above keeps track of all non-dominated solutions and Figure 1 shows how these improve over time w.r.t. all objectives (two in that example). Let’s now discuss how LEMONADE overcomes the need for training all networks from scratch. The key idea here is that LEMONADE re-uses weights of already trained parent networks for the children rather than training the children from scratch. To do so, we frame our mutations as network morphisms. Network morphisms are function-preserving operators on the space of neural networks, meaning that the function a neural network computes does not change when applying these operators. This implies that network morphisms also preserve the performance of a neural network. So, say you trained a neural network and it has 90% accuracy. Now you want to add another layer to your network and you do so by employing a network morphism. Then, your new network already starts at 90% – by construction! Hence, you don’t need to train it from scratch. Rather, you just need to fine-tune it for a few iterations. How does this work? Well, firstly, all our mutations only change small parts of the network architecture locally, meaning we can simply copy most weights from the parent network and only need to worry about the part of the network that actually changes. Let’s say you want to add a layer without changing the function that the network computes; then, your newly added layers need to be an identity mapping. Here’s a very simple example: say your network is composed of a single convolution layer, followed by a ReLU activation function and some softmax output layer:
where w_{1,1} denote the weights the softmax layer and w_{1,2} the weights of the convolutional layer. Now we want to add another ReLU-Conv block, so the new network should look like this:
with weight tensors w_{2,1}, w_{2,2} , w_{2,3}. As a first step, we simply copy all weights of unchanged layers, i.e., we set
Next, we want the other conv layer to be an identity mapping, which can fortunately be achieved by properly fillingw2,2 with 0’s and 1’s. What about the remaining new ReLU function? Actually, we don’t need to care about it, since the ReLU function is idempotent (i.e., ReLU (ReLU (x) = ReLU (x)). Let’s have a look at our new network:
Hence, N_2(x) is actually computing the same function as N_1(x). We can achieve this function-preserving property for many other operations, such as increasing the number of filters, adding skip connections or other non-linear building blocks. There are also tricks to deal with operations that shrink the networks, which we call approximate network morphisms.
To further speed up the search, we also exploit that in our setting some objectives are very expensive to evaluate (e.g., evaluating the performance of a network requires training), while others are very cheap (e.g., counting the number of parameters or flops). We do so by having a sampling strategy for parents and mutations based on the cheap objectives only, which further speeds up LEMONADE by spending more resources on children that are more likely to improve the population. The sampling process is illustrated and explained more detailed in Figure 2.
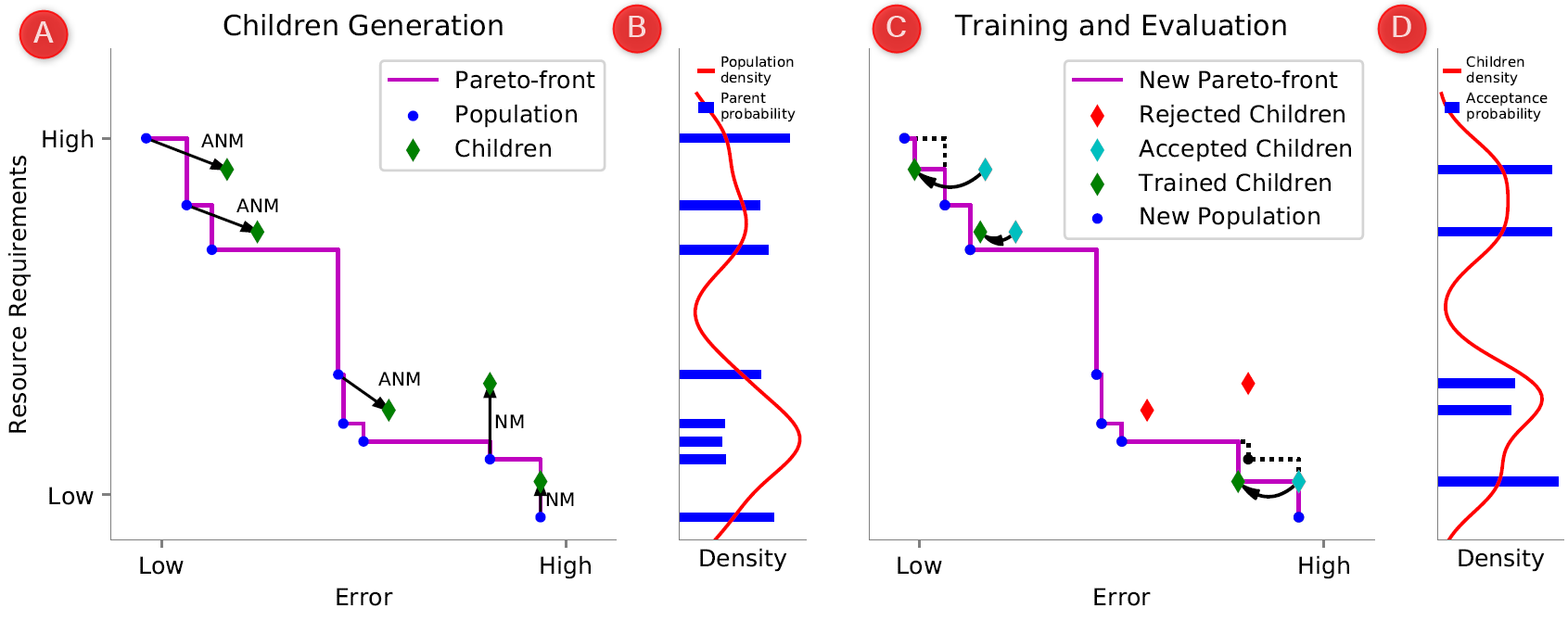
Figure 2. A: error rate (expensive objective) is plotted on the x-axis, and resource requirements (cheap objectives) on the y-axis. Blue dots denote the current population, resulting in the purple Pareto-front. Parents generate children (green diamonds) by applying mutations by means of (approximate) network morphism (ANM, NM). Therefore, a child’s error is the same (in the case of NM) or close to (ANM) to its parent’s error. NM in general increase resource requirements, ANM decrease them (at the cost of a higher error). B: sampling distribution of parents. LEMONADE computes a density over the current population (red curve) with respect to the cheap objectives (resource requirements). Networks from the population are chosen as parents with a probability anti-proportional to the density estimation (blue bars). C: A subset of the children is accepted for training (cyan diamonds), potentially improving the Pareto-front after fine-tuning (green diamonds), while other children are rejected and not being trained (red diamonds). D: the subset sampling is again based on a density estimation, illustrated here.
Figure 3 shows some results from running LEMONADE on Cifar, where we optimized five objectives: error on Cifar-10, error on Cifar-100, number of parameters, number of multiply-add operations and inference time. LEMONADE achieves competitive performance compared to prior work on single-objective NAS employing RL (NASNet), while being approximately 30 times faster, and to MobileNets V2, which are manually constructed networks specifically designed for efficiency. Especially in the low resource regime, one can see that LEMONADE outperforms the baselines as these are not specifically designed to work well in these regimes while LEMONADE is.
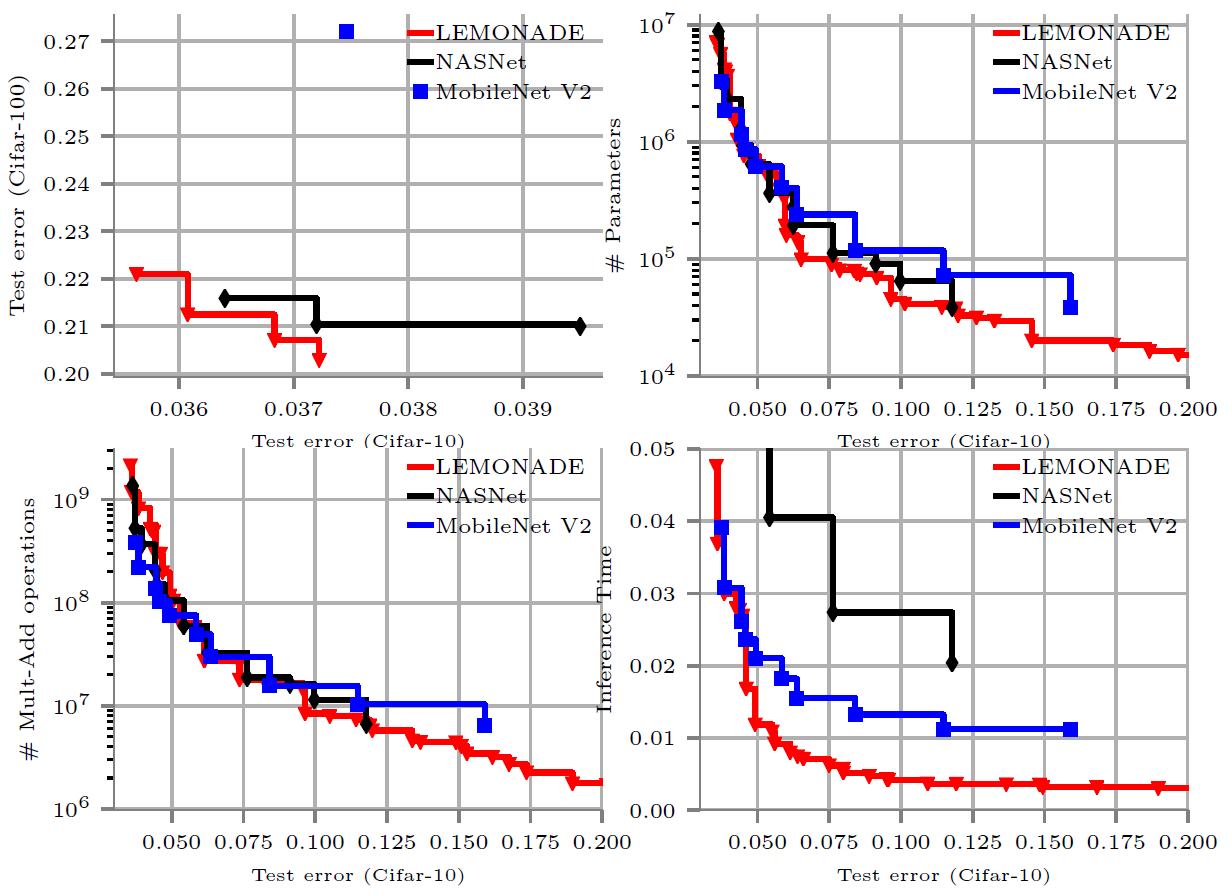
Figure 3. Results after running LEMONADE on Cifar with the five objectives 1) error on Cifar-10 (x-axis in all plots), 2) error on Cifar-100 (y-axis, top left), 3) number of parameters (top right), number of multiply-add operations (bottom left) and inference time (bottom right).
With LEMONADE, we developed a method for not only improving the state of the art by designing large and complex neural networks, but rather a method for automatically finding architectures well suited for practical applications by considering multiple objectives concurrently. We hope this will make Deep Learning more broadly applicable for a broad range of applications. Interested in more details? Check out the paper. Also see our other recent NAS papers.