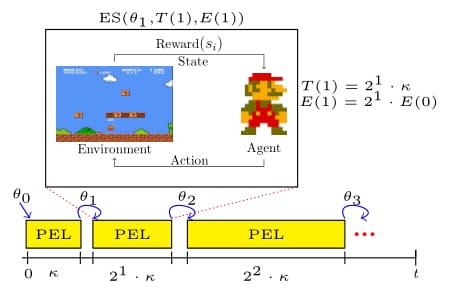
A framework of ES-based limited episode’s length
Evolutionary Strategy for Reinforcement Learning
Recently, evolutionary strategy(ES) showed surprisingly good performance as an alternative approach to deep Reinforcement Learning algorithms for playing Atari games [1, 2, 3]. ES directly optimizes the weights of deep policy networks encoding a mapping from states to actions. Thus, an ES approach for RL consists of optimizing a population of policies in the spaces of potentially millions of network weights.
The advantages of ES compared to gradient-based optimizers are that (i) ES is a gradient-free black-box approach which is able to optimize non-differentiable functions, and more importantly, (ii) ES can be efficiently parallelized resulting in short optimization time compared to sequential optimizers and many deep RL-algorithms [1].
Progressive Episode Lengths
Inspired by the human strategy to first learn short and easy tasks, before learning the hard tasks, we propose to use progressive episode lengths (PEL), i.e., first train an agent to play short episodes and then based on the experience gained on these short episodes, train an agent on longer episodes.
The PEL approach is based on incremental learning, where an agent utilizes the capabilities obtained in limited games to an entire episodic run. The goal of this approach is to achieve a more stable and faster optimization process by focusing on simpler and shorter tasks first. When integrating it with canonical ES, the latter is able to optimize by only playing a portion of a game, transferring the abilities obtained in a short game to a longer one. For example in the game of Pong, by solely learning to hit the ball, the algorithm could learn to play an entire game.
Another important advantage of the proposed PEL is that the ES approach can evaluate more policies by playing shorter games and thus, it can potentially make progress much faster. This applies in particular to tasks in RL, since the most time-consuming step is often the evaluation of policies and not the ES-update of the policies.
For the case of Atari games, these games typically last until the player loses all its in-game lives, which can take quite some time in certain games even if only a simple policy is applied. Therefore, limited episode lengths for evaluating more policies can speed up the optimization process substantially.
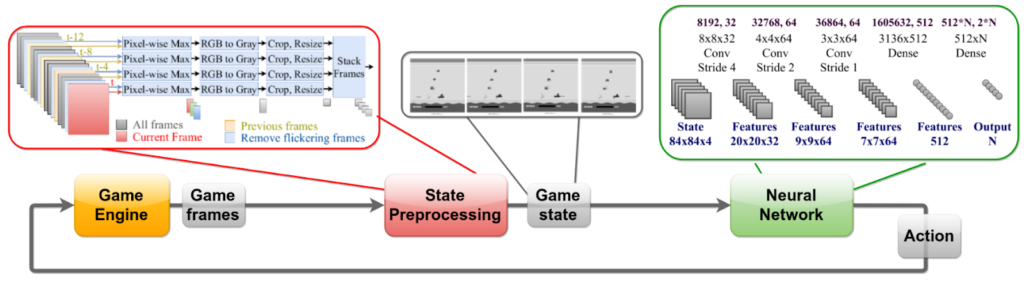
Figure 2: Playing Atari games using Deep Neural Networks following Chrabaszcz et al.
Episode Scheduler
One of the main components of PEL is the episode scheduler to determine how many steps an episode should have at most. Partially following the idea of successive halving by [4], we propose a simple, yet effective episode scheduler that doubles the maximal episode length in each step. In preliminary experiments, we observed that in practice an important design decision is how to initialize the episode scheduler with E(0) similar to the important minimal budget in successive halving and approaches build upon it [5, 6]. For playing Atari games, we found that using the expected number of steps in playing random games is a good first estimate for E(0). However, on some games even more aggressive strategies can be beneficial such that we initialize E(0) by the expected number of steps in playing random games divided by a constant; we used 2 in our experiments. To approximate the expectation, we used Monte-Carlo roll-outs.
Time Scheduler
The second main component of PEL is the time scheduler T(n) defining how long to run ES given a limited episode length E(n). We propose two simple but yet effective schedulers.
The first scheduler Tc simply uses the time uniformly, i.e., T(n) is constant (in our experiments, we used 1 hour).
The second schedule Td is again motivated by successive halving [4] such that we double the time budget in each iteration, i.e., for some user-defined (20min in our experiments). Using the second scheduler combined with our proposed episode scheduler, PEL will spend half of its overall optimization budget on the maximal episode length. Therefore, even if our heuristic assumption of learning on short games how to play long games should not hold, PEL will still focus on long games for most of its optimization budget.
How does PEL compare to the canonical ES for playing Atari games?
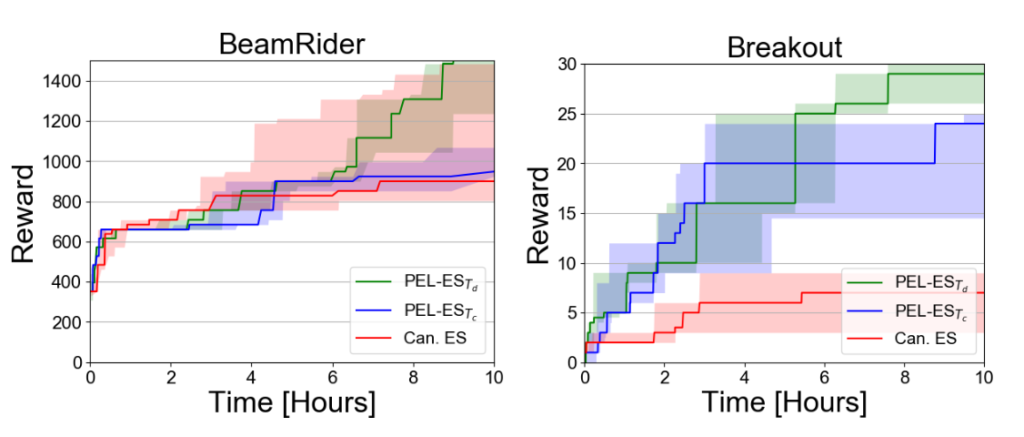
After 2 hours of training, the PEL approach with both schedulers outperformed the canonical ES in 5 and 6 games out of 9 and improved the scores by 49% and 80% on average, respectively. This shows the effectiveness of using the proposed PEL approach to improve the performance of canonical ES by optimizing different episode lengths, and utilizing the best-so-far policy of the previous iteration to improve further. After 10 hours, both schedulers are better than canonical ES in 7 out of 9 games, with an average improvement of 28% and 32% respectively. We conjecture that by running canonical ES for a longer time, the effect of PEL evaluating more policies decreases in comparison, such that the average improvement drops. On the other hand, PEL increases the episode lengths more often by running for 10 hours such that the PEL is more robust in this setting. (Please note that PEL with Tc increased the episode length only once within 2 hours).
Figure 3: Score over time for PEL (blue Tc and green Td) and canonical ES (red). Each line is the median score of 5 optimization runs and the shaded areas show the 25% and 75% percentiles of these runs.
How well do the proposed time schedulers perform?
Comparing both schedulers, Td performed better in 6 out of 9 games both after 2 and 10 hours. The average improvement of Td after 2 hours is much higher than Tc‘s, but it is quite similar after 10 hours.
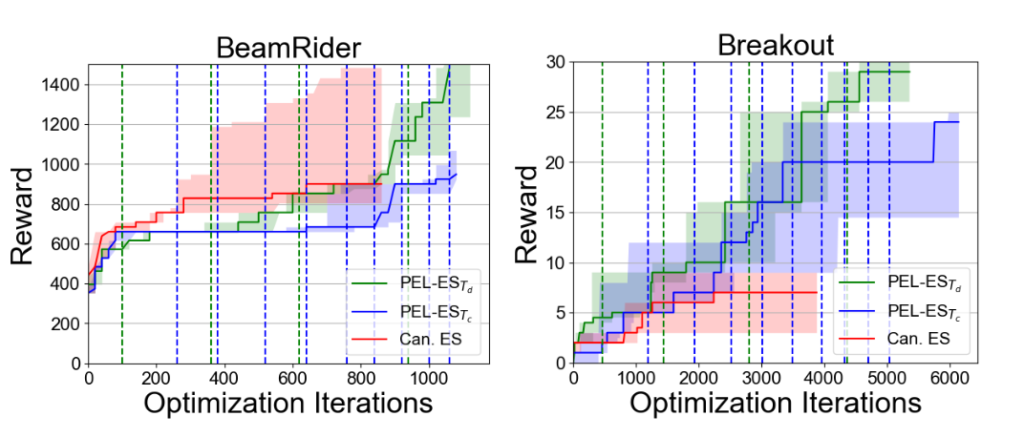
To study the performance of both approaches over time in more detail, Figure 3 shows the performance of the best-so-far found policy evaluated on the full game lengths at each time point. Td performed particularly well after the first 5 hours and benefited from running longer games later on more than Tc. We draw a similar conclusion from studying the performance over the number of iterations (i.e., updates of the population), as shown in Figure 4.
Figure 4: Score over time for PEL (Tc and Td) and canonical ES. Each line is the median score of 5 optimization runs and the shaded areas show the 25% and 75% percentiles of these runs. The vertical lines show the points after which the maximal episode lengths were increased.
Is it possible to learn well-performing policies for long games by training only on short games?
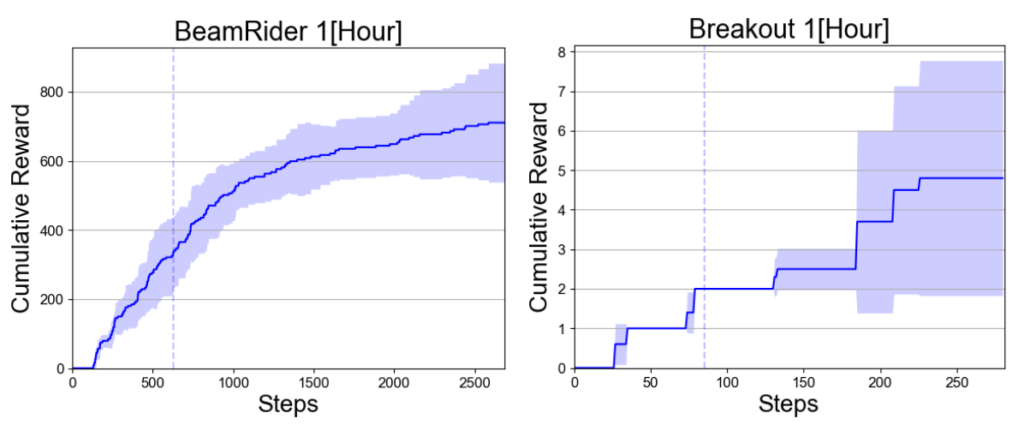
In order to verify whether an agent can learn a reasonable policy on short games, we studied the performance of PEL with Tc after 2 hours. At this point, PEL has not seen the full game, as shown in Figure 5 by the vertical lines. Nevertheless, PEL was able to find policies that played well on these short games (until the vertical line), but which are also able to perform well if we let them continue playing the games (after the vertical line). This verifies that the policies found by ES generalize to longer games and therefore, PEL is an efficient approach on these games.
Figure 5: Mean of cumulative reward for 30 evaluation runs for PEL with Tc with 2 hours time budget. The red dashed line indicates the maximal number of actions observed by PEL
Take Home Message
The PEL approach has several assumptions: (i) We can find a well-performing policy on short games that generalizes well to longer games. We showed that this holds for many Atari games with dense reward signals. (ii) We initialize our minimal episode length by playing random games. For games with a survival component, this often provides a reasonable starting point. Future work will include finding a more reliable heuristic to initialize episode lengths for different kinds of tasks, and to start the evolution from different game fragments instead of playing the game from the beginning all the time.
If you are interested to learn more about the method, check out the paper
References
[1] T. Salimans, J. Ho, X. Chen, and S. Sidor amd I. Sutskever.
Evolution strategies as a scalable alternative to reinforcement learning
In arXiv:1703.03864 [stat.ML], 2017.
[2] E. Conti, V. Madhavan, F. Such, J. Lehman, K. Stanley, and J. Clune.
Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents
In arXiv:1712.06560 [cs.AI]
[3] P. Chrabaszcz, I. Loshchilov, and F. Hutter.
Back to basics: Benchmarking canonical evolution strategies for playing atari
In Proc. of IJCAI, pages 1419–1426, 2018.
[4] Z. Karnin, T. Koren, and O. Somekh.
Almost optimal exploration in multi-armed bandits
In Proc. of ICML, pages 1238–1246, 2013.
[5] L. Li, K. Jamieson, G. DeSalvo, A. Rostamizadeh, and A. Talwalkar.
Hyperband: A novel banditbased approach to hyperparameter optimization
Journal of Machine Learning Research, 18:185:1–185:52, 2017.
[6] S. Falkner, A. Klein, and F. Hutter.
BOHB: robust and efficient hyperparameter optimization
at scale. In Proc. of ICML, pages 1436–1445, 2018.